
【題目】如圖,己知函數y=﹣ ![]() x+4的圖象與坐標軸的交點分別為點A、B,點C與點B關于x軸對稱,動點P、Q分別在線段BC、AB上(點P不與點B、C重合).且∠APQ=∠ABO
x+4的圖象與坐標軸的交點分別為點A、B,點C與點B關于x軸對稱,動點P、Q分別在線段BC、AB上(點P不與點B、C重合).且∠APQ=∠ABO
(1)點A的坐標為 , AC的長為;
(2)判斷∠BPQ與∠CAP的大小關系,并說明理由;
(3)當△APQ為等腰三角形時,求點P的坐標.
【答案】
(1)(3,0),5
(2)解:∠BPQ=∠CAP.理由如下:
∵點C與點B關于x軸對稱,
∴AB=AC,
∴∠ABC=∠ACB,
∵∠APQ=∠ABC,
∴∠ACB=∠APQ,
∵∠BPA=∠ACB+∠CAP,
即∠BPQ+∠APQ=∠ACB+∠CAP,
∴∠BPQ=∠CAP;
(3)解:當PA=PQ,如圖1,則∠PQA=∠PAQ,
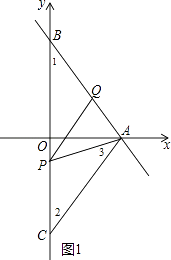
∵∠PQA=∠1+∠BPQ=∠APQ+∠BPQ=∠BPA,
∴BP=BA=5,
∴OP=BP﹣OB=1,
∴P(0,﹣1);
當AQ=AP,則∠AQP=∠APQ,
而∠AQP=∠BPA,所以此情況不存在;
當QA=QP,如圖2,則∠APQ=∠PAQ,
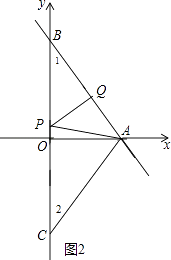
而∠1=∠APQ,
∴∠1=∠PAQ,
∴PA=PB,
設P(0,t),則PB=4﹣t,
∴PA=4﹣t,
在Rt△OPA中,∵OP2+OA2=PA2,
∴t2+32=(4﹣t)2,解得t= ![]() ,
,
∴P(0, ![]() ),
),
綜上所述,滿足條件的P點坐標為(0,﹣1),(0, ![]() ).
).
【解析】解:(1)當y=0時,﹣ ![]() x+4=0,解得x=3,則A(3,0),
x+4=0,解得x=3,則A(3,0),
當x=0時,y=﹣ ![]() x+4=4,則B(0,4),
x+4=4,則B(0,4),
∵點C與點B關于x軸對稱,
∴C(0,﹣4),
∴AC= ![]() =5;
=5;
所以答案是(3,0),5;
【考點精析】本題主要考查了三角形的外角和勾股定理的概念的相關知識點,需要掌握三角形一邊與另一邊的延長線組成的角,叫三角形的外角;三角形的一個外角等于和它不相鄰的兩個內角的和;三角形的一個外角大于任何一個和它不相鄰的內角;直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2才能正確解答此題.


科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c (a≠0)的圖象如圖所示,有下列5個結論:
①abc<0; ②b<a+c; ③4a+2b+c>0;④2c<3b;⑤a+b<m (am+b)(m≠1的實數),其中結論正確的個數有( )
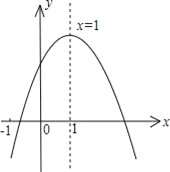
A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩車從A地出發沿同一路線駛向B地,甲車先出發勻速駛向B地.40分鐘后,乙車出發,勻速行駛一段時間后,在途中的貨站裝貨耗時半小時,由于滿載貨物,為了行駛安全,速度減少了50千米/時,結果與甲車同時到達B地.甲乙兩車距A地的路程y(千米)與乙車行駛時間x(小時)之間的函數圖象如圖所示.
請結合圖象信息解答下列問題:
(1)直接寫出a的值,并求甲車的速度;
(2)求圖中線段EF所表示的y與x的函數關系式,并直接寫出自變量x的取值范圍;
(3)乙車出發多少小時與甲車相距15千米?直接寫出答案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,P是菱形ABCD的對角線AC上一動點,過P垂直于AC的直線交菱形ABCD的邊于M、N兩點,設AC=2,BD=1,AP=x,△AMN的面積為y,則y關于x的函數圖象的大致形狀是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知如圖1:△ABC中,AB=AC,∠B、∠C的平分線相交于點O,過點O作EF∥BC交AB、AC于E、F.
(1)圖中有幾個等腰三角形?請說明EF與BE、CF間有怎樣的關系. 
(2)若AB≠AC,其他條件不變,如圖2,圖中還有等腰三角形嗎?如果有,請分別指出它們.另第(1)問中EF與BE、CF間的關系還存在嗎?
(3)若△ABC中,∠B的平分線與三角形外角∠ACD的平分線CO交于O,過O點作OE∥BC交AB于E,交AC于F.如圖3,這時圖中還有哪幾個等腰三角形?EF與BE、CF間的關系如何?為什么? 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】動漫節開幕前,某動漫公司預測某種動漫玩具能夠暢銷,就分兩批分別用32000元和68000元購進了這種玩具銷售,其中第二批購進數量是第一批購進數量的2倍,但每套進價多了10元.
(1)該動漫公司這兩批各購進多少套玩具?
(2)如果這兩批玩具每套售價相同,且全部銷售后總利潤不少于20000元,那么每套售價至少是多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com