
【題目】如圖,已知直線y=![]() x與雙曲線y=
x與雙曲線y=![]() (k>0)交于A、B兩點,點B的坐標為(﹣4,﹣2),C為雙曲線y=
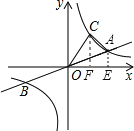
(k>0)交于A、B兩點,點B的坐標為(﹣4,﹣2),C為雙曲線y=![]() (k>0)上一點,且在第一象限內,若△AOC的面積為6,則點C的坐標為 .
(k>0)上一點,且在第一象限內,若△AOC的面積為6,則點C的坐標為 .

【答案】(2,4)或(8,1)
【解析】
試題分析:把點B的坐標代入反比例函數解析式求出k值,再根據反比例函數圖象的中心對稱性求出點A的坐標,然后過點A作AE⊥x軸于E,過點C作CF⊥x軸于F,設點C的坐標為(a,![]() ),然后根據S△AOC=S△COF+S梯形ACFE﹣S△AOE列出方程求解即可得到a的值,從而得解.
),然后根據S△AOC=S△COF+S梯形ACFE﹣S△AOE列出方程求解即可得到a的值,從而得解.
解:∵點B(﹣4,﹣2)在雙曲線y=![]() 上,
上,
∴![]() =﹣2,
=﹣2,
∴k=8,
根據中心對稱性,點A、B關于原點對稱,
所以,A(4,2),
如圖,過點A作AE⊥x軸于E,過點C作CF⊥x軸于F,設點C的坐標為(a,![]() ),
),
若S△AOC=S△COF+S梯形ACFE﹣S△AOE,
=![]() ×8+
×8+![]() ×(2+
×(2+![]() )(4﹣a)﹣
)(4﹣a)﹣![]() ×8,
×8,
=4+![]() ﹣4,
﹣4,
=![]() ,
,
∵△AOC的面積為6,
∴![]() =6,
=6,
整理得,a2+6a﹣16=0,
解得a1=2,a2=﹣8(舍去),
∴![]() =
=![]() =4,
=4,
∴點C的坐標為(2,4).
若S△AOC=S△AOE+S梯形ACFE﹣S△COF=![]() ,
,
∴![]() =6,
=6,
解得:a=8或a=﹣2(舍去)
∴點C的坐標為(8,1).
故答案為:(2,4)或(8,1).



科目:初中數學 來源: 題型:
【題目】計算:
(1)3c3-2c2+8c-13c3+2c-2c2+3;
(2)8x2-4(2x2+3x-1);
(3)5x2-2(3y2-5x2)+(-4y2+7xy).
查看答案和解析>>
科目:初中數學 來源: 題型:
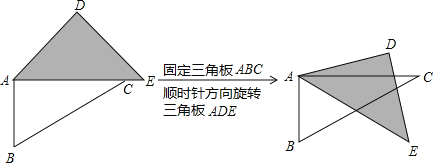
【題目】如圖1,將三角板ABC與三角板ADE擺放在一起;如圖2,固定三角板ABC,將三角板ADE繞點A按順時針方向旋轉,記旋轉角∠CAE=α(0°<α<180°).當△ADE的一邊與△ABC的某一邊平行(不共線)時,寫出旋轉角α的所有可能的度數為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
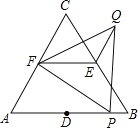
【題目】如圖,△ABC和△FPQ均是等邊三角形,點D、E、F分別是△ABC三邊的中點,點P在AB邊上,連接EF、QE.若AB=6,PB=1,則QE= .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】請認真觀察圖形,解答下列問題:
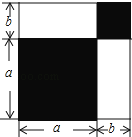
(1)根據圖中條件,用兩種方法表示兩個陰影圖形的面積的和(只需表示,不必化簡);
(2)由(1),你能得到怎樣的等量關系?請用等式表示;
(3)如果圖中的a,b(a>b)滿足a2+b2=53,ab=14,求:①a+b的值;②a4﹣b4的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com