
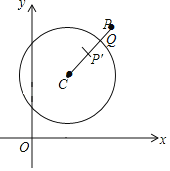
【題目】如圖,在平面直角坐標系xOy 中,點P是⊙C外一點,連接CP交⊙C于點Q,點P關于點Q的對稱點為P′,當點P′在線段CQ上時,稱點P為⊙C“友好點”.已知A(1,0),B(0,2),C(3,3)
(1)當⊙O的半徑為1時,
①點A,B,C中是⊙O“友好點”的是 ;
②已知點M在直線y=﹣![]() x+2 上,且點M是⊙O“友好點”,求點M的橫坐標m的取值范圍;
x+2 上,且點M是⊙O“友好點”,求點M的橫坐標m的取值范圍;
(2)已知點D![]() ,連接BC,BD,CD,⊙T的圓心為T(t,﹣1),半徑為1,若在△BCD上存在一點N,使點N是⊙T“友好點”,求圓心T的橫坐標t的取值范圍.
,連接BC,BD,CD,⊙T的圓心為T(t,﹣1),半徑為1,若在△BCD上存在一點N,使點N是⊙T“友好點”,求圓心T的橫坐標t的取值范圍.
【答案】(1)①B;②0≤m≤![]() ;(2)﹣4+3
;(2)﹣4+3![]() ≤t<3
≤t<3![]()
【解析】
(1))①根據“友好點”的定義,OB=2r=2,所以點B是⊙O“友好點”;
②設M(m,﹣![]() m+2 ),根據“友好點”的定義,OM=
m+2 ),根據“友好點”的定義,OM=![]()
![]() ,解得0≤m≤
,解得0≤m≤![]() ;
;
(2)B(0,2),C(3,3),D![]() ,⊙T的圓心為T(t,﹣1),點N是⊙T“友好點”,NT≤2r=2,所以點N只能在線段BD上運動,過點T作TN⊥BD于N,作TH∥y軸,與BD交于點H.易知∠BDO=30°,∠OBD=60°,NT=
,⊙T的圓心為T(t,﹣1),點N是⊙T“友好點”,NT≤2r=2,所以點N只能在線段BD上運動,過點T作TN⊥BD于N,作TH∥y軸,與BD交于點H.易知∠BDO=30°,∠OBD=60°,NT=![]() HT,直線BD:y=﹣
HT,直線BD:y=﹣![]() x+2,H(t,﹣
x+2,H(t,﹣![]() t+2 上),HT=﹣
t+2 上),HT=﹣![]() t+2﹣(﹣1)=﹣
t+2﹣(﹣1)=﹣![]() t+3,NT=
t+3,NT=![]() HT=
HT=![]() (﹣
(﹣![]() t+3)=﹣
t+3)=﹣![]() t+
t+![]() ,解出t的范圍.
,解出t的范圍.
解:(1)①∵r=1
∴根據“友好點”的定義,OB=2r=2
∴點B是⊙O“友好點”
OC=3![]() >2r,不是⊙O“友好點”
>2r,不是⊙O“友好點”
A(1,0)在⊙O上,不是⊙O“友好點”
故答案為B;
②如圖,
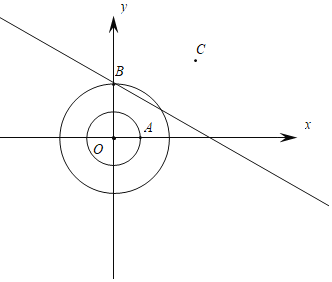
設M(m,﹣![]() m+2 ),根據“友好點”的定義
m+2 ),根據“友好點”的定義
∴OM=![]()
整理,得2m2﹣2![]() m≤0
m≤0
解得0≤m≤![]() ;
;
∴點M的橫坐標m的取值范圍:0≤m≤![]() ;
;
(2)∵B(0,2),C(3,3),D![]() ,⊙T的圓心為T(t,﹣1),點N是⊙T“友好點”
,⊙T的圓心為T(t,﹣1),點N是⊙T“友好點”
∴NT≤2r=2,
∴點N只能在線段BD上運動,過點T作TN⊥BD于N,作TH∥y軸,與BD交于點H.
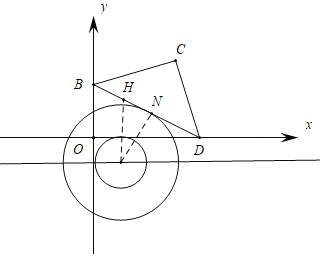
易知∠BDO=30°,
∴∠OBD=60°,
∴NT=![]() HT,
HT,
∵B(0,2),D![]() ,
,
∴直線BD:y=﹣![]() x+2,H(t,﹣
x+2,H(t,﹣![]() t+2 上),
t+2 上),
∴HT=﹣![]() t+2﹣(﹣1)=﹣
t+2﹣(﹣1)=﹣![]() t+3,
t+3,
∴NT=![]() HT=
HT=![]() (﹣
(﹣![]() t+3)=﹣
t+3)=﹣![]() t+
t+![]() ,
,
∴﹣![]() t+
t+![]() ≤2,
≤2,
∴t≥﹣4+![]() ,
,
當H與點D重合時,點T的橫坐標等于點D的橫坐標,即t=![]() ,
,
此時點N不是“友好點”,
∴t<![]() ,
,
故圓心T的橫坐標t的取值范圍:﹣4+![]() ≤t<
≤t<![]() .
.


科目:初中數學 來源: 題型:
【題目】一個不透明的袋子里有若干個小球,它們除了顏色外,其它都相同,甲同學從袋子里隨機摸出一個球,記下顏色后放回袋子里,搖勻后再次隨機摸出一個球,記下顏色,…,甲同學反復大量實驗后,根據白球出現的頻率繪制了如圖所示的統計圖,則下列說法正確的是( )
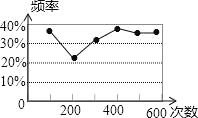
A. 袋子一定有三個白球
B. 袋子中白球占小球總數的十分之三
C. 再摸三次球,一定有一次是白球
D. 再摸1000次,摸出白球的次數會接近330次
查看答案和解析>>
科目:初中數學 來源: 題型:
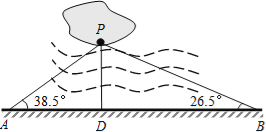
【題目】如圖,益陽市梓山湖中有一孤立小島,湖邊有一條筆直的觀光小道AB,現決定從小島架一座與觀光小道垂直的小橋PD,小張在小道上測得如下數據:AB=80.0米,∠PAB=38.5°,∠PBA=26.5.請幫助小張求出小橋PD的長并確定小橋在小道上的位置.(以A,B為參照點,結果精確到0.1米)
(參考數據:sin38.5°=0.62,cos38.5°=0.78,tan38.5°=0.80,sin26.5°=0.45,cos26.5°=0.89,tan26.5°=0.50)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,AB>AD,∠A=60°,
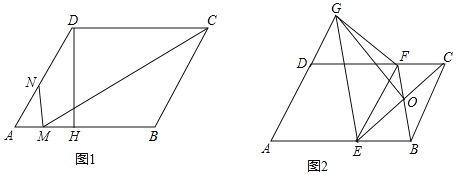
(1)如圖1,過點D作DH⊥AB于點H,MC平分∠DCB交AB邊于點M,過M作MN⊥AB交AD邊于點N,AN:ND=2:3,平行四邊形ABCD的面積為60![]() ,求MN的長度.
,求MN的長度.
(2)如圖2,E、F分別為邊AB、CD上一點,且AE=AD=DF,連接BF、EC交于點O,G為AD延長線上一點,連接GE、GF和GO,若∠GFD=∠EFB,求證:GO⊥EC.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1的小正方形組成的網格中,△ABC的三個頂點均在格點上.將△ABC繞點A順時針旋轉90°得到△AB1C1.
(1)在網格中畫出△AB1C1;
(2)計算點B旋轉到B1的過程中所經過的路徑長.(結果保留π)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料,回答問題.
材料:求圓外一定點到圓上距離最小值是安徽省中考數學較為常見的一種題型,此類題型試題有時出題者將圓隱藏,故又稱為“隱圓問題”.解決這類問題,關鍵是要找到動點的運動軌跡,即該動點是繞哪一個定點旋轉,且能保持旋轉半徑不變.從而找到動點所在的隱藏圓,進面轉換成圓外一點到圓心的距離減半徑,求得最小值.
解決問題:
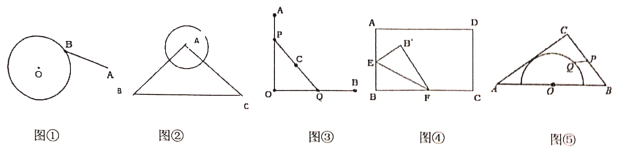
(1)如圖①,圓O的半徑為1,圓外一點A到圓心的距離為3,圓上一動點B,當A、O、B滿足條件____________時,![]() 有最小值為____________.
有最小值為____________.
(2)如圖②,等腰![]() 兩腰長為5,底邊長為6,以A為圓心,2為半徑作圓,圓上動點P到
兩腰長為5,底邊長為6,以A為圓心,2為半徑作圓,圓上動點P到![]() 的距離最小值為__________.
的距離最小值為__________.
(3)如圖③,![]() ,P、Q分別是射線
,P、Q分別是射線![]() 、
、![]() 上兩個動點,C是線段
上兩個動點,C是線段![]() 的中點,且
的中點,且![]() ,則在線段
,則在線段![]() 滑動的過程中,求點C運動形成的路徑長,并說明理由.
滑動的過程中,求點C運動形成的路徑長,并說明理由.
(4)如圖④,在矩形![]() 中,
中,![]() ,
,![]() ,點E是
,點E是![]() 中點,點F是
中點,點F是![]() 上一點,把
上一點,把![]() 沿著
沿著![]() 翻折,點B落在點
翻折,點B落在點![]() 處,求
處,求![]() 的最小值,并說明理由.
的最小值,并說明理由.
(5)如圖⑤,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,以邊
,以邊![]() 中點O為圓心,作半圓與
中點O為圓心,作半圓與![]() 相切,點P,Q分別是邊
相切,點P,Q分別是邊![]() 和半圓上的動點,連接
和半圓上的動點,連接![]() ,求
,求![]() 長的最小值,并說明理由.
長的最小值,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某游樂園有一個直徑為16米的圓形噴水池,噴水池的周邊有一圈噴水頭,噴出的水柱為拋物線,在距水池中心3米處達到最高,高度為5米,且各方向噴出的水柱恰好在噴水池中心的裝飾物處回合,如圖所示,以水平方向為![]() 軸,噴水池中心為原點建立平面直角坐標系.
軸,噴水池中心為原點建立平面直角坐標系.
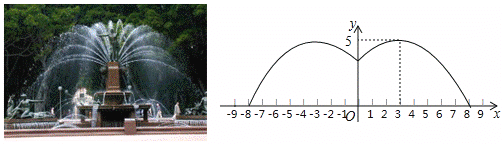
(1)求水柱所在拋物線(第一象限部分)的函數表達式;
(2)王師傅在噴水池內維修設備期間,噴水管意外噴水,為了不被淋濕,身高1.8米的王師傅站立時必須在離水池中心多少米以內?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,有一座拋物線形拱橋,在正常水位時水面AB的寬為20米,如果水位上升3米,則水面CD的寬是10米.
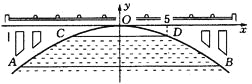
(1)建立如圖所示的直角坐標系,求此拋物線的解析式;
(2)當水位在正常水位時,有一艘寬為6米的貨船經過這里,船艙上有高出水面3.6米的長方體貨物(貨物與貨船同寬).問:此船能否順利通過這座拱橋?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com