Question

【題目】如圖，在△ABC中，∠ABC和∠ACB的平分線相交于點G，過點G作EF∥BC交AB于E，交AC于F，過點G作GD⊥AC于D，下列四個結論： ①EF=BE+CF；
②∠BGC=90°+ ∠A；
③點G到△ABC各邊的距離相等；
④設GD=m，AE+AF=n，則S△AEF=mn．
其中正確的結論是 ．

Answer 1

【答案】①②③
【解析】解：①∵∠ABC和∠ACB的平分線相交于點G， ∴∠EBG=∠CBG，∠BCG=∠FCG．
∵EF∥BC，
∴∠CBG=∠EGB，∠BCG=∠CGF，
∴∠EBG=∠EGB，∠FCG=∠CGF，
∴BE=EG，GF=CF，
∴EF=EG+GF=BE+CF，故本小題正確；
②∵∠ABC和∠ACB的平分線相交于點G，
∴∠GBC+∠GCB= （∠ABC+∠ACB）= （180°﹣∠A），
∴∠BGC=180°﹣（∠GBC+∠GCB）=180°﹣ （180°﹣∠A）=90°+ ∠A，故本小題正確；
③∵∠ABC和∠ACB的平分線相交于點G，
∴點G是△ABC的內心，
∴點G到△ABC各邊的距離相等，故本小題正確；
④連接AG，
∵點G是△ABC的內心，GD=m，AE+AF=n，
∴S△AEF= AEGD+ AFGD= （AE+AF）GD= nm，故本小題錯誤．
所以答案是：①②③．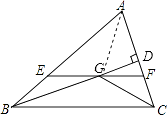

【考點精析】關于本題考查的平行線的性質和角平分線的性質定理，需要了解兩直線平行，同位角相等；兩直線平行，內錯角相等；兩直線平行，同旁內角互補；定理1：在角的平分線上的點到這個角的兩邊的距離相等； 定理2：一個角的兩邊的距離相等的點，在這個角的平分線上才能得出正確答案．