
【題目】如圖,平面直角坐標(biāo)系中,點(diǎn)M是直線y=2與x軸之間的一個動點(diǎn),且點(diǎn)M是拋物線y= ![]() +bx+c的頂點(diǎn),則拋物線y=
+bx+c的頂點(diǎn),則拋物線y= ![]() +bx+c與直線y=1交點(diǎn)的個數(shù)是( )
+bx+c與直線y=1交點(diǎn)的個數(shù)是( ) 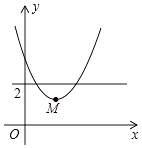
A.0個或1個
B.0個或2個
C.1個或2個
D.0個、1個或2個
【答案】D
【解析】解:由拋物線y=x2+bx+c的圖象可知,該拋物線與x軸沒有交點(diǎn), 即:△<0,
則:b2﹣4c<0,
又點(diǎn)M是直線y=2與x軸之間的一個動點(diǎn),點(diǎn)M的坐標(biāo)為:(﹣ ![]() ,
, ![]() ),
),
所以,0< ![]() <2,即:﹣8<b2﹣4c<0,
<2,即:﹣8<b2﹣4c<0,
令y=x2+bx+c﹣1,則要求方程x2+bx+c=1的解得個數(shù),只需判定拋物線y=x2+bx+c﹣1與x軸有無交點(diǎn)及交點(diǎn)的個數(shù)即可.
又因為,△=b2﹣4ac=b2﹣4(c﹣1)=b2﹣4c+4,
所以,﹣4<b2﹣4c+4<4,
即:①當(dāng)﹣4<b2﹣4c+4<0時,拋物線y=x2+bx+c﹣1與x軸沒有交點(diǎn);②b2﹣4c+4=0時,拋物線y=x2+bx+c﹣1與x軸有一個交點(diǎn);③0<b2﹣4c+4<4時,拋物線y=x2+bx+c﹣1與x軸有兩個交點(diǎn).
故選:D.
【考點(diǎn)精析】根據(jù)題目的已知條件,利用二次函數(shù)的性質(zhì)的相關(guān)知識可以得到問題的答案,需要掌握增減性:當(dāng)a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當(dāng)a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】小明早晨從家里出發(fā)勻速步行去上學(xué),小明的媽媽在小明出發(fā)后10分鐘,發(fā)現(xiàn)小明的數(shù)學(xué)課本沒帶,于是她帶上課本立即勻速騎車按小明上學(xué)的路線追趕小明,結(jié)果與小明同時到達(dá)學(xué)校.已知小明在整個上學(xué)途中,他出發(fā)后t分鐘時,他所在的位置與家的距離為s千米,且s與t之間的函數(shù)關(guān)系的圖象如圖中的折線段OA﹣AB所示. 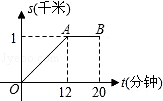
(1)試求折線段OA﹣AB所對應(yīng)的函數(shù)關(guān)系式;
(2)請解釋圖中線段AB的實(shí)際意義;
(3)請在所給的圖中畫出小明的媽媽在追趕小明的過程中,她所在位置與家的距離s(千米)與小明出發(fā)后的時間t(分鐘)之間函數(shù)關(guān)系的圖象.(友情提醒:請對畫出的圖象用數(shù)據(jù)作適當(dāng)?shù)臉?biāo)注)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知,如圖,AB是⊙O的直徑,點(diǎn)C為⊙O上一點(diǎn),OF⊥BC于點(diǎn)F,交⊙O于點(diǎn)E,AE與BC交于點(diǎn)H,點(diǎn)D為OE的延長線上一點(diǎn),且∠ODB=∠AEC. 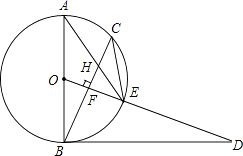
(1)求證:BD是⊙O的切線;
(2)求證:CE2=EHEA;
(3)若⊙O的半徑為 ![]() ,sinA=
,sinA= ![]() ,求BH的長.
,求BH的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分別是BG,AC的中點(diǎn).
(1)求證:DE=DF,DE⊥DF;
(2)連接EF,若AC=10,求EF的長.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平整的地面上,10個完全相同的棱長為8cm的小正方體堆成一個幾何體.
(1)在下面的網(wǎng)格中畫出從左面看和從上面看的形狀圖.

(2)如果在這個幾何體的表面(不含底面)噴上黃色的漆,則這個幾何體噴漆的面積是多少cm2.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】求一個正數(shù)的算術(shù)平方根,有些數(shù)可以直接求得,如![]() ,有些數(shù)則不能直接求得,如
,有些數(shù)則不能直接求得,如![]() ,但可以通過計算器求. 還有一種方法可以通過一組數(shù)的內(nèi)在聯(lián)系,運(yùn)用規(guī)律求得,請同學(xué)們觀察下表:
,但可以通過計算器求. 還有一種方法可以通過一組數(shù)的內(nèi)在聯(lián)系,運(yùn)用規(guī)律求得,請同學(xué)們觀察下表:
n | 16 | 0.16 | 0.0016 | 1600 | 160000 | … |
| 4 | 0.4 | 0.04 | 40 | 400 | … |
(1)若![]() ,則
,則![]()
(2)根據(jù)你發(fā)現(xiàn)的規(guī)律,探究下列問題:已知![]() ≈1.435,則:
≈1.435,則:
①![]() ≈ ;
≈ ;
②![]() ≈ ;
≈ ;
(3)根據(jù)上述探究過程類比研究一個數(shù)的立方根已知![]() ≈1.260,則
≈1.260,則![]() ≈ .
≈ .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知:如圖,在△ABC中,AB=AC,D為邊BC上一點(diǎn),以AB,BD為鄰邊作平行四邊形ABDE,連接AD,EC. 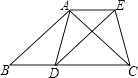
(1)求證:AD=CE;
(2)當(dāng)點(diǎn)D在什么位置時,四邊形ADCE是矩形,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】下列圖形是將正三角形按一定規(guī)律排列,則第4個圖形中所有正三角形的個數(shù)有( )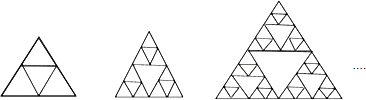
A.160
B.161
C.162
D.163
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com