
【題目】已知:等邊![]() 中.
中.
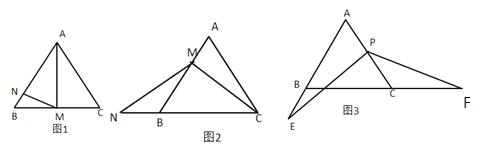
(1)如圖1,點![]() 是
是![]() 的中點,點
的中點,點![]() 在
在![]() 邊上,滿足
邊上,滿足![]() ,求
,求![]() 的值.
的值.
(2)如圖2,點![]() 在
在![]() 邊上(
邊上(![]() 為非中點,不與
為非中點,不與![]() 、
、![]() 重合),點
重合),點![]() 在
在![]() 的延長線上且
的延長線上且![]() ,求證:
,求證:![]() .
.
(3)如圖3,點![]() 為
為![]() 邊的中點,點
邊的中點,點![]() 在
在![]() 的延長線上,點
的延長線上,點![]() 在
在![]() 的延長線上,滿足
的延長線上,滿足![]() ,求
,求![]() 的值.
的值.
【答案】(1)3;(2)見解析;(3)![]() .
.
【解析】
(1)先證明![]() ,
,![]() 與
與![]() 均為直角三角形,再根據直角三角形中
均為直角三角形,再根據直角三角形中![]() 所對的直角邊等于斜邊的一半,證明BM=2BN,AB=2BM,最后轉化結論可得出BN與AN之間的數量關系即得;
所對的直角邊等于斜邊的一半,證明BM=2BN,AB=2BM,最后轉化結論可得出BN與AN之間的數量關系即得;
(2)過點M作ME∥BC交AC于E,先證明AM=ME,再證明![]() 與
與![]() 全等,最后轉化邊即得;
全等,最后轉化邊即得;
(3)過點P作PM∥BC交AB于M,先證明M是AB的中點,再證明![]() 與
與![]() 全等,最后轉化邊即得.
全等,最后轉化邊即得.
(1)∵![]() 為等邊三角形,點
為等邊三角形,點![]() 是
是![]() 的中點
的中點
∴AM平分∠BAC,![]() ,
,![]()
∴![]() ,
,![]()
∵![]()
∴![]() ,
,![]()
∴![]()
∴![]()
∴在![]() 中,
中,![]()
在![]() 中,
中,![]()
∴![]()
∴![]() 即
即![]() .
.
(2)如下圖:
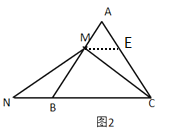
過點M作ME∥BC交AC于E
∴∠CME=∠MCB,∠AEM=∠ACB
∵![]() 是等邊三角形
是等邊三角形
∴∠A=∠ABC=∠ACB=![]()
∴![]() ,
,![]()
∴![]() ,
,![]()
∴AM=ME
∵![]()
∴∠CME=∠MNB,MN=MC
∴在![]() 與
與![]() 中
中
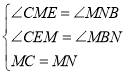
∴![]()
∴![]()
∴![]()
(3)如下圖:
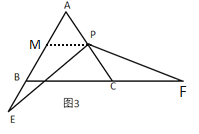
過點P作PM∥BC交AB于M
∴![]()
∵![]() 是等邊三角形
是等邊三角形
∴∠A=∠ABC=∠ACB=![]() ,
,![]()
∴![]()
∴![]() ,
,![]() ,
,![]()
∴![]() 是等邊三角形,
是等邊三角形,![]()
∴![]()
∵P點是AC的中點
∴![]()
∴![]()
在![]() 與
與![]() 中
中
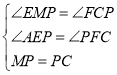
∴![]()
∴![]()
∴![]()
∴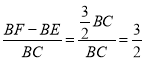 .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,∠ABC=75°,E為BC延長線上一點,∠ABC與∠ACE的平分線相交于點D.則∠D的度數為( )

A.15°B.17.5°C.20°D.22.5°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,△ABC是等邊三角形,AE=CD,BQ⊥AD于Q,BE交AD于點P,下列說法:①∠APE=∠C,②AQ=BQ,③BP=2PQ,④AE+BD=AB,其中正確的個數有( )個。
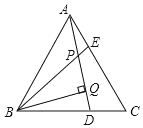
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中數學 來源: 題型:
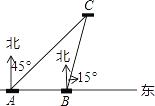
【題目】如圖,某日在我國某島附近海域有兩艘自西向東航行的海監船A、B,船在A船的正東方向,且兩船保持20海里的距離,某一時刻兩海監船同時測得在A的東北方向,的北偏東15°方向有一我國漁政執法船C,求此時船C與船B的距離是多少.(結果保留小數點后一位)
參考數據: ![]() ≈1.414,
≈1.414, ![]() ≈1.732,
≈1.732, ![]() ≈2.236.
≈2.236.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列一段文字,然后回答下列問題.
已知平面內兩點 M(x1,y1)、N(x2,y2),則這兩點間的距離可用下列公式計算: MN= ![]() .
.
例如:已知 P(3,1)、Q(1,﹣2),則這兩點間的距離 PQ=![]() =
=![]() .
.
特別地,如果兩點 M(x1,y1)、N(x2,y2)所在的直線與坐標軸重合或平行于坐標軸或垂直于坐 標軸,那么這兩點間的距離公式可簡化為 MN=丨 x1﹣x2 丨或丨 y1﹣y2 丨.
(1)已知 A(1,2)、B(﹣2,﹣3),試求 A、B 兩點間的距離;
(2)已知 A、B 在平行于 x 軸的同一條直線上,點 A 的橫坐標為 5,點 B 的橫坐標為﹣1,
試求 A、B 兩 點間的距離;
(3)已知△ABC 的頂點坐標分別為 A(0,4)、B(﹣1,2)、C(4,2),你能判定△ABC 的形狀 嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一次函數 y=kx+b 的圖象經過點(-1,-5),且與正比例函數![]() 于點(2,a),求:
于點(2,a),求:
(1)a 的值;
(2)k,b 的值;
(3)這兩個函數圖象與 x 軸所圍成的三角形的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知像這樣由7個全等的正六邊形組成的圖形叫做“二環蜂窩”,每個正六邊形的頂點叫做格點,頂點都在格點上的三角形叫做格點三角形.已知△ABC為該二環蜂窩一個格點三角形,則在該二環蜂窩中,以點A為頂點且與△ABC相似(包括全等但不與△ABC重合)的格點三角形最多能作的個數為( )
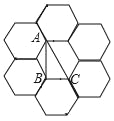
A. 18 B. 23 C. 25 D. 28
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,C為線段AE上一動點(不與點A、E重合),在AE同側分別作正△ABC和正△CDE,AD與BE交于點O,AD與BC交于點P,BE與CD交于點Q,連接PQ.以下五個結論:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.
恒成立的結論有 .(把你認為正確的序號都填上)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在讀書月活動中,學校準備購買一批課外讀物.為使課外讀物滿足同學們的需求,學校就“我最喜愛的課外讀物”從文學、藝術、科普和其他四個類別進行了抽樣調查(每位同學只選一類),如圖是根據調查結果繪制的兩幅不完整的統計圖.

請你根據統計圖提供的信息,解答下列問題:
(1)本次調查中,一共調查了 名同學;
(2)條形統計圖中,m= ,n= ;
(3)扇形統計圖中,藝術類讀物所在扇形的圓心角是 度;
(4)學校計劃按文學、藝術、科普和其他四個類別購買課外讀物 9000 冊,請根據樣本數據,估計學校購買其他類讀物 冊比較合理.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com